검색결과 리스트
그래프에 해당되는 글 1건
- 2012.07.10 C 로 구현한 알고리즘 - 2부 자료 구조, 11장 그래프(Graph)
글
C 로 구현한 알고리즘 - 2부 자료 구조, 11장 그래프(Graph)
AVL 트리와 RB 트리 공부하다가 진이 빠져서, 몇 일 책을 못봤다.
결국 RB 트리를 구현하긴 했지만, 왜 했나 싶기도 하고...
이번엔 자료구조의 마지막 장, Graph 이다.
시작
|
(출처: http://en.wikipedia.org/wiki/File:6n-graf.svg )
위 그림이 컴퓨터 사이언스에서 이야기 하는 Graph 자료구조를 그림으로 표현한 것이다.
그림에는 따로 방향성이 없는데, 방향성을 가지는 (즉, 가운데 선이 화살표 모양으로 표시될 수 있는)
Graph 도 있다.
Graph는 객체들 사이의 관계나 연결에 따라 정의되는 문제들을 모델링하는 데 주로 사용된다.
객체는 정점(Vertex)으로 표시되고 객체들 사이의 관계나 연결은 정점들 정점들 사이의 에지(Edge)로 표현된다.
그래프의 탐색방법은 Vertex 를 특성 순서로 방문하는 기법이다.
여기에는 Breadth-First Search(BFS)와 Depth-First Search(DFS)가 있다.
이 글에서는 Graph 와 Graph traversal(그래프 탐색방법)에 대해서 알아 볼 것이다.
그래프는 다음과 같은 어플리케이션에서 사용된다.
- 그래프 알고리즘
- 네트워크 홉(hop) 세기- 위상 정렬: 예를들면, 와우의 스킬트리를 Linear List 로 만드는 것이랄까...
- 그래프 색칠하기: 각 Edge로 연결된 Vertex는 서로 다른 색을 칠하는 문제. 이 기준을 만족시키는 최소의 색 수를
Chromatic number라 한다.
- 해밀턴 사이클 문제: 한 Vertex에서 출발하여 모든 Vertex들을 한 번씩만 방문하여 시작 Vertex로 돌아오는 사이클을
해밀턴 사이클 이라고 한다.
TSP(Traveling Salesman Problem, 외판원 여행 문제)가 해밀턴 사이클 문제의 특수한 경우.
- 클릭 문제: Clique(클릭)이란, Undirected Graph 'G' 의 Vertex들로 이루어진 집합이 있을 때, 이 집합의 임의의
두 Vertex가 모두 Edge로 연결되어 있다면 이 집합을 Clique이라 한다.
예를들면, 오각형 안에 별이 그려져 있는 그래프를 생각해 보라.
- 충돌 직렬화: (설명이 좀 힘들어 패스. 사실 나도 어렴풋이 감이 오는 정도이기도 하고..;;)
그래프(Graph)
Graph는 두 가지 요소, Vertex와 Edge로 이루어진다.
Vertex는 객체를 의미하고 Edge는 객체들 사이의 관계나 연결을 말한다.
또한 Graph는 Directed(방향성)/Undirected(무방향성)이 있다.
Directed Graph는 Edge를 화살표로 표시한다. 때로는 이 Edge를 Arc라고 부르기도 한다.
Directed Graph에서 Cycle이 없는 Graph를 Directed Acyclic Graph(DAG)라고 한다.
Edge는 라벨이나 숫자값과 같은 Edge value를 가질 수도 있다.
Graph의 기본 인터페이스는 다음 링크에서 확인 할 수 있다.
http://en.wikipedia.org/wiki/Graph_%28data_structure%29#Operations
(Vertex 추가/삭제 인터페이스도 필요하다면 추가를 해야 할 것이다)
Graph는 두 개의 다른 자료구조료 표현할 수 있다.
List 와 Matrix 이다.
두 개의 큰 차이는 Adjacent vertex들를 List로 표현하는가 Matrix로 표현하는가의 차이이다.
List로 표현하는 방법은 쉽게 머리속에 상상할 수 있다. (Adjacency List)
Matrix로 표현하는 방법은 아래 그림과 같다. (Adjacency Matrix)
 |
|
(출처: http://en.wikipedia.org/wiki/Adjacency_matrix#Examples )
그림과 같은 Row 1 은 Vertex 1 와 연결된 Adjacent vertex들을 나타낸다.
Undirected Graph는 Matrix가 대칭적으로 나타난다.
Directed Graph에서 1 --> 2 라면, (Row 1, Col 2)는 1 이고, (Row 2, Col 1)은 0 이 될 것이다.
이 두가지는 어떤 차이점이 있을까?
| Adjacency list | Adjacency Matrix |
|
| 저장공간 |
O(V+E) |
O(V^2) |
| Vertex 추가 |
O(1) | O(V^2) |
| Edge 추가 |
O(1) | O(1) |
Vertex 삭제 |
O(E) |
O(V^2) |
| Edge 삭제 |
O(E) | O(1) |
Vertex u와 v가 인접한가? (단, u와 v의 저장위치는 알고 있다) |
O(V) | O(1) |
| 특징 | Vertex나 Edge를 삭제할 때, 모든 Vertex들이나 Edge들을 찾아야 할 필요가 있다. 일반적으로 Sparse graph에 효율적이다. |
Vertex를 추가/삭제하기 위해서는, Matrix가 Resize/Copy되어야 하므로 느리다.
graph가 dense할 때 사용한다. ( E가 V^2에 가까울 수록... ) |
(V는 Vertex들의 갯수, E는 Edge들의 갯수)
그래프 탐색(Graph traversal)
Graph의 Vertex들을 특정 순서대로 한 번씩 방문하는 것을 말한다.
여기에는 두 가지 방법이 있는 데, 너비 우선(Breadth-first) 탐색과 깊이 우선(Depth-first) 탐색이 있다.
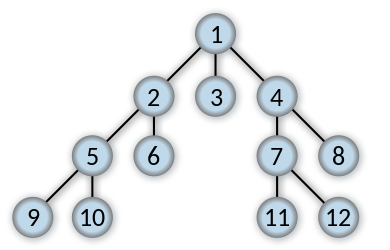
- Breadth-First Search(BFS)
Graph 를 더 탐험하기 전에 한 정점에 인접한 정점들을 먼저 방문하는 것이다.
|
(Author: Alexander Drichel, 출처 : http://en.wikipedia.org/wiki/File:Breadth-first-tree.svg )
위 Graph의 Vertex에 적힌 숫자가 방문 순서이다.
BSF는 최소 신장 트리(minimum spanning trees)와 최단 경로(shortest paths) 등, 많은 어플리케이션에 유용하다.
그 외에도 http://en.wikipedia.org/wiki/Breadth-first_search#Applications 여기에서 여러가지 적용의 예를 볼수 있다.
BSF의 구현을 Pseudocode 로 작성해 보면 다음과 같다.
G: a graph, v: root of G
(All verties are colored with white at starting)
function BFS(G, v):
Queue Q;;
v.setColor(gray);
Q.enqueue(v);
while ( NOT Q.isEmpty() )
t = Q.dequeue();
t.setColor(black);
for each ( x in G.adjacentVerties(t) )
if ( x.getColor() == white )
o.setColor(gray);
Q.enqueue(o);
- Depth-First Search(DFS)
Graph를 탐색할 때, 한 브랜치를 따라 가능한 멀리까지 먼저 방문하는 것이다.
 |
(Author: Alexander Drichel, 출처:http://en.wikipedia.org/wiki/File:Depth-first-tree.svg )
DFS는 사이틀 탐지(cycle detection)와 위상 정렬(topological sorting)을 포함한 많은 어플리케이션에 유용하다.
그 외에도 http://en.wikipedia.org/wiki/Depth-first_search#Applications 여기에서 다른 적용 예를 볼 수 있다.
특히 DFS를 이용하여 미로를 만드는 것은 비디오로 감상해 볼 수 있다.
DFS의 구현을 Pseudocode 로 작성해 보면 다음과 같다.
G: a graph, v: root of G
(All verties are colored with white at starting)
function DFS(G, v):
v.setColor(gray);
for each ( x in G.adjacentVerties(v) )
if ( x.getColor() == white )
call DFS(G, x);
v.setColor(black)
결론
Graph 자체는 별로 어렵지 않은 듯 한데...
책에도 적혀 있듯이, 아주 유연한 자료구조이다.
그래서인지 Java API 에도 STL 에도 Graph 자료구조는 없다.
이 후의 Graph 알고리즘에서 좀 더 사용해보면 익숙해 지겠지..
'공부' 카테고리의 다른 글
| [알고리즘] P, NP, NP-Complete, NP-Hard (0) | 2012.07.16 |
|---|---|
| C 로 구현한 알고리즘 - 3부 알고리즘에 들어가기 전에... (1) | 2012.07.16 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |