검색결과 리스트
트리에 해당되는 글 1건
- 2012.07.03 C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree)
글
C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree)
트리에 대한 자료를 찾으면서 우선 위키피디아를 한 번 쭉 읽어 봤다.
그 중 바이너리 트리의 마지막 부분(http://en.wikipedia.org/wiki/Binary_tree#External_links)을 보면
'Trees in computer science' 를 보면 엄청난 종류의 트리들이 나온다.
이걸 보면서 느낀 건, "아, 정말 사람들이 치열하게 고민을 했구나...' 하는 것이다.
약간의 성능 향상이라도 얻기 위해 이 부분, 저 부분 고민을 한 흔적이 느껴졌다.
( 이 수많은 트리들이 그냥 나온건 아니니깐... )
마음 같아선 저 모든 트리들의 특징을 정리해 보고 싶지만... 그건 힘들것 같고,
일반적으로 트리를 사용하는 이유(효율적인 탐색!!!)에 집중해서 정리해 본다.
트리(Tree)
먼저 아래 그림을 보자.
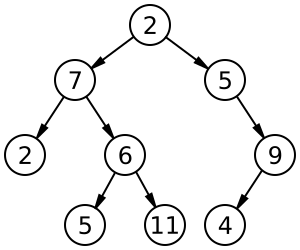
( http://en.wikipedia.org/wiki/File:Binary_tree.svg )
이미지로 표현을 하자면 위와 같은 모양으로 자료가 저장되는 자료구조가 트리(Tree)다.
트리에서 사용하는 용어들은 다음과 같다.
- 노드(Node): 위 그림에서 데이터 및 다른 데이터를 가리키는 포인터를 포함해서 노드(Node)라고 한다.
- 루트(Root): 트리에서 제일 상위에 있는 노드를 루트라고 한다.
- 자식(Child): 한 노드의 바로 아래(포인터를 가지고 있는) 노드를 말한다.
- 부모(Parent): 한 노드의 바로 상위 노드를 말한다.
- 분기 계수(branching factor): 한 노드가 가질 수 있는 자식의 최대 수를 말한다.
- 형제(sibling): 부모의 다른 자식 노드들이다.
- 자손(descendant): 한 노드에서 뻗어나간 하위의 모든 노드들을 말한다.
- 조상(ancestor): 한 노드와 루트 간의 경로에 있는 모든 노드들이다.
- 높이(height): 노드들이 존재하는 단계의 수. 트리의 높이. 예를 들면 위 그림의 높이는 4 이다.
- 리프 노드(Left Node): 자식이 없는 노드.
기본적인 용어들은 머 이 정도?
트리는 다음과 같은 곳에서 사용된다.
- 허프만 코딩: 자료 집합을 압축하는데 사용하는데 허프만 트리를 사용하는 자료 압축 방법
- 프로그램 메뉴
- 데이터베이스 시스템
- 식 처리: 컴파일러나 휴대용 계산기에서 자주 수행되는 작업이다.
- 우선순위 큐
이 글의 이후 내용은 다음과 같은 내용을 다루겠다.
- 바이너리 트리(Binary Tree, 이진트리)
- 순회 방법(Travesal)
- 트리 평형,
- 바이너리 서치 트리(BST, Binary Serarch Tree, 이진탐색트리)
- 그 외 주제에 대해서
바이너리 트리(Binary Tree, 이진 트리)
자식을 2개까지 가질 수 있는 노드들로 이루어진 트리다.
광범위하게 사용되며, 더 복잡한 트리 구조체의 토대도 된다.
순회 방법들(Traversal)
트리의 노드들을 방문하는 순서에 대한 내용이다.
- preorder (전위 순회) : Parent -> Left -> Right
- inorder (중위 순회) : Left -> Parent -> Right
- postorder (후위 순회) : Left -> Right -> Parent
앞에 접두사가 현재 노드의 방문 순서를 가리킨다고 생각하면 된다.
그리고 노드의 방문은 Recursive 하게 방문한다.
바이너리 서치 트리(Binary Search Tree, BST, 이진 탐색 트리)
탐색을 위해 특별히 구조화된 이진 트리이다.
부모보다 작은 노드는 왼쪽 자손에 부모보다 큰 노드는 오른쪽 자손에 위치한다.

( http://en.wikipedia.org/wiki/File:Binary_search_tree.svg )
예를 들면, 위 그림과 같이 트리를 구성하게 된다.
BST 의 탐색 속도는 트리가 평형을 유지한다면 O(lg n)이 된다.
(트리 평형을 이룬다는 말은 트리의 주어진 노드의 갯수에 대해 트리의 높이를 짧게 유지한다는 것이다)
트리가 균형을 이루지 못한다면 최악의 경우 O(n)이 된다.
이 차이는 매우 큰 데, 2^16 개의 데이터를 검색할 때
O(lg n)는 최대 16번, O(n)은 최대 65,536번의 탐색이 필요하다.
여기까지는 솔직히 별로 어렵지 않다.
하지만 트리의 평형을 어떻게 유지하는 가에 대한 문제로 들어가면 쉽지 않다.
트리 평형(Tree Balancing)
위에서 잠깐 언급했듯이,
트리 평형이란 주어진 노드들의 개수에 대해 트리의 높이를 가능한 짧게 유지하는 것이다.
트리의 평형은 데이터 서치의 성능에 영향을 미친다.
바이너리 트리에 노드를 Insert, Delete 할 때, Balancing 을 유지하는 트리에는 여러 방법이 있다.
이러한 트리들을 Self-balancing binary search tree 라고 한다.
( http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree )
위키피디아에는 위와 같은 트리들에 대해서 언급하고 있다.
Selft-balancing binary search tree 들 중 하나 정도는 외우고 싶은데,
머가 제일 쉬운지 모르겠다.
그 외 트리에 대해...
- 수식의 표현
바이너리 트리는 탐색에 특화된 것으로 보이지만,
다른 곳에도 응용이 가능하다.
예를 들면 수식을 표현하는 데, 좋은 방법이 된다.
- 트라이(Trie)
가변 길이 문자열 집합을 탐색하는 데 주로 사용된다.

( http://en.wikipedia.org/wiki/File:Trie_example.svg )
- B-Tree
( B-Tree 는 Binary Tree 가 아니다. 혼동하지 말자. )
보조 기억장치에 저장된 자료에 접근하는 성능을 향상시키기 위해서
대체로 데이터베이스 시스템에서 사용하는 탐색 트리다.
B-Tree에 대한 자세한 내용은 http://en.wikipedia.org/wiki/B-tree 을 참고.결론
글의 처음에 이야기 했듯이 많은 종류의 트리들이 있다.
그리고 각각의 트리들은 저마다 특징이 있다.
많은 종류덕에 이 특징들을 모두 기억하기도 쉽지 않다.
내가 생각하는 트리의 핵심은 이거다.
1. 데이터의 크기를 비교할 수 있는 데이터를 검색하는 데는 바이너리 서치 트리가 좋다.
2. 바이너리 서치 트리라면 가능하면 기본적으로 Self-balancing 이 되도록 해야 한다.
3. 다뤄야 하는 데이터의 갯수가 많다면, 그 때의 상황에 맞는 특화된 트리를 찾아본다.
4. 탐색과 관계없는 자료도 트리로 표현하는 게 좋을 때가 있다. (수식이나 디렉토리, 메뉴 처럼...)
이게 정답은 아닐수도 있겠지만, 내가 트리를 써야 할 일이 있다면...
위와 같이 고민을 하다가, 라이브러리를 찾겠지. -_-;
( 내가 특별한 상황에 있지 않는 이상 Reinvention 할 필요는 없겠지 )
마지막으로 인터넷을 검색하다가, 트리에 대한 좋은 글들이 있는 블로그를 발견했다.
http://sweeper.egloos.com/category/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0/page/3
나는 머 내 맘대로 날림 수준으로 복습해 놓은거지만,
이 분은 상당히 자세히 적어 두었다.
하나 더, http://webdiis.unizar.es/asignaturas/EDA/AVLTree/avltree.html 에 가면
Self-Balancing Binary Search Tree 과정을 시각적으로 볼 수 있다.
(2012.7.4 추가)
self-balancing search tree 의 대표적인 두 가지 방법
AVL Tree 와 RB(red-black) Tree 중 어느 것이 좋은가?
실제 나의 기억으로도 자료 구조 시간에 저 두 개의 트리에 대해서 집중적으로 배운거 같긴 하다.
결론부터 말하면 RB Tree 를 더 선호하는 것 같다.
실제로 Java 의 TreeMap 과 C++ STL std::map 에서 self-balancing search tree 의 구현은 모두
RB Tree 로 되어 있다고 한다.
http://stackoverflow.com/questions/5288320/why-is-stdmap-implemented-as-red-black-tree
위 글의 답변을 인용해 보면,
AVL Tree 는 최대 1.44 lg(n) 이지만 RB Tree 는 최대 2 lg(n) 이라고 한다.
그럼에도 불구하고, RB Tree 를 쓰는 이유는
삽입/삭제 후의 Re-balancing 에 드는 코스트 때문이란다.
AVL Tree 의 경우 O(lg n) 이지만, RB Tree 는 O(1) 이다.
그래서 빈번한 RB Tree 가 search 에 조금 약 할지라도,
삽입/삭제에서 훨씬 강하니... RB Tree 를 선택한게 아닐까?
(2012.7.5 추가)
둘 다 구현하다가 시간 문제로 포기.
아.. 학교다닐 때 열심히 할 껄... 이라는 생각도 해 봤지만,
어짜피 기억 안나는건 같았을껄?
AVL 은 Balacing-Factor 를 가지고 Re-balancing 을 하고,
RB Tree 는 red-black properties 에 따라 Re-balancing 을 한단다.
후.. 나중에 필요하면 다시 공부하자.
* RB-Tree 는 http://en.wikipedia.org/wiki/Red%E2%80%93black_tree 에
상세하게 설명되어 있다. 약간만 더 손보면 되는 코드와 함께!
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 11장 그래프(Graph) (0) | 2012.07.10 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |