글
C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree)
트리에 대한 자료를 찾으면서 우선 위키피디아를 한 번 쭉 읽어 봤다.
그 중 바이너리 트리의 마지막 부분(http://en.wikipedia.org/wiki/Binary_tree#External_links)을 보면
'Trees in computer science' 를 보면 엄청난 종류의 트리들이 나온다.
이걸 보면서 느낀 건, "아, 정말 사람들이 치열하게 고민을 했구나...' 하는 것이다.
약간의 성능 향상이라도 얻기 위해 이 부분, 저 부분 고민을 한 흔적이 느껴졌다.
( 이 수많은 트리들이 그냥 나온건 아니니깐... )
마음 같아선 저 모든 트리들의 특징을 정리해 보고 싶지만... 그건 힘들것 같고,
일반적으로 트리를 사용하는 이유(효율적인 탐색!!!)에 집중해서 정리해 본다.
트리(Tree)
먼저 아래 그림을 보자.
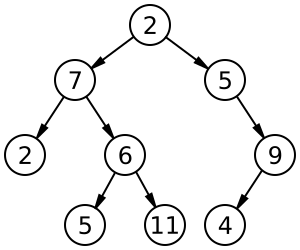
( http://en.wikipedia.org/wiki/File:Binary_tree.svg )
이미지로 표현을 하자면 위와 같은 모양으로 자료가 저장되는 자료구조가 트리(Tree)다.
트리에서 사용하는 용어들은 다음과 같다.
- 노드(Node): 위 그림에서 데이터 및 다른 데이터를 가리키는 포인터를 포함해서 노드(Node)라고 한다.
- 루트(Root): 트리에서 제일 상위에 있는 노드를 루트라고 한다.
- 자식(Child): 한 노드의 바로 아래(포인터를 가지고 있는) 노드를 말한다.
- 부모(Parent): 한 노드의 바로 상위 노드를 말한다.
- 분기 계수(branching factor): 한 노드가 가질 수 있는 자식의 최대 수를 말한다.
- 형제(sibling): 부모의 다른 자식 노드들이다.
- 자손(descendant): 한 노드에서 뻗어나간 하위의 모든 노드들을 말한다.
- 조상(ancestor): 한 노드와 루트 간의 경로에 있는 모든 노드들이다.
- 높이(height): 노드들이 존재하는 단계의 수. 트리의 높이. 예를 들면 위 그림의 높이는 4 이다.
- 리프 노드(Left Node): 자식이 없는 노드.
기본적인 용어들은 머 이 정도?
트리는 다음과 같은 곳에서 사용된다.
- 허프만 코딩: 자료 집합을 압축하는데 사용하는데 허프만 트리를 사용하는 자료 압축 방법
- 프로그램 메뉴
- 데이터베이스 시스템
- 식 처리: 컴파일러나 휴대용 계산기에서 자주 수행되는 작업이다.
- 우선순위 큐
이 글의 이후 내용은 다음과 같은 내용을 다루겠다.
- 바이너리 트리(Binary Tree, 이진트리)
- 순회 방법(Travesal)
- 트리 평형,
- 바이너리 서치 트리(BST, Binary Serarch Tree, 이진탐색트리)
- 그 외 주제에 대해서
바이너리 트리(Binary Tree, 이진 트리)
자식을 2개까지 가질 수 있는 노드들로 이루어진 트리다.
광범위하게 사용되며, 더 복잡한 트리 구조체의 토대도 된다.
순회 방법들(Traversal)
트리의 노드들을 방문하는 순서에 대한 내용이다.
- preorder (전위 순회) : Parent -> Left -> Right
- inorder (중위 순회) : Left -> Parent -> Right
- postorder (후위 순회) : Left -> Right -> Parent
앞에 접두사가 현재 노드의 방문 순서를 가리킨다고 생각하면 된다.
그리고 노드의 방문은 Recursive 하게 방문한다.
바이너리 서치 트리(Binary Search Tree, BST, 이진 탐색 트리)
탐색을 위해 특별히 구조화된 이진 트리이다.
부모보다 작은 노드는 왼쪽 자손에 부모보다 큰 노드는 오른쪽 자손에 위치한다.

( http://en.wikipedia.org/wiki/File:Binary_search_tree.svg )
예를 들면, 위 그림과 같이 트리를 구성하게 된다.
BST 의 탐색 속도는 트리가 평형을 유지한다면 O(lg n)이 된다.
(트리 평형을 이룬다는 말은 트리의 주어진 노드의 갯수에 대해 트리의 높이를 짧게 유지한다는 것이다)
트리가 균형을 이루지 못한다면 최악의 경우 O(n)이 된다.
이 차이는 매우 큰 데, 2^16 개의 데이터를 검색할 때
O(lg n)는 최대 16번, O(n)은 최대 65,536번의 탐색이 필요하다.
여기까지는 솔직히 별로 어렵지 않다.
하지만 트리의 평형을 어떻게 유지하는 가에 대한 문제로 들어가면 쉽지 않다.
트리 평형(Tree Balancing)
위에서 잠깐 언급했듯이,
트리 평형이란 주어진 노드들의 개수에 대해 트리의 높이를 가능한 짧게 유지하는 것이다.
트리의 평형은 데이터 서치의 성능에 영향을 미친다.
바이너리 트리에 노드를 Insert, Delete 할 때, Balancing 을 유지하는 트리에는 여러 방법이 있다.
이러한 트리들을 Self-balancing binary search tree 라고 한다.
( http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree )
위키피디아에는 위와 같은 트리들에 대해서 언급하고 있다.
Selft-balancing binary search tree 들 중 하나 정도는 외우고 싶은데,
머가 제일 쉬운지 모르겠다.
그 외 트리에 대해...
- 수식의 표현
바이너리 트리는 탐색에 특화된 것으로 보이지만,
다른 곳에도 응용이 가능하다.
예를 들면 수식을 표현하는 데, 좋은 방법이 된다.
- 트라이(Trie)
가변 길이 문자열 집합을 탐색하는 데 주로 사용된다.

( http://en.wikipedia.org/wiki/File:Trie_example.svg )
- B-Tree
( B-Tree 는 Binary Tree 가 아니다. 혼동하지 말자. )
보조 기억장치에 저장된 자료에 접근하는 성능을 향상시키기 위해서
대체로 데이터베이스 시스템에서 사용하는 탐색 트리다.
B-Tree에 대한 자세한 내용은 http://en.wikipedia.org/wiki/B-tree 을 참고.결론
글의 처음에 이야기 했듯이 많은 종류의 트리들이 있다.
그리고 각각의 트리들은 저마다 특징이 있다.
많은 종류덕에 이 특징들을 모두 기억하기도 쉽지 않다.
내가 생각하는 트리의 핵심은 이거다.
1. 데이터의 크기를 비교할 수 있는 데이터를 검색하는 데는 바이너리 서치 트리가 좋다.
2. 바이너리 서치 트리라면 가능하면 기본적으로 Self-balancing 이 되도록 해야 한다.
3. 다뤄야 하는 데이터의 갯수가 많다면, 그 때의 상황에 맞는 특화된 트리를 찾아본다.
4. 탐색과 관계없는 자료도 트리로 표현하는 게 좋을 때가 있다. (수식이나 디렉토리, 메뉴 처럼...)
이게 정답은 아닐수도 있겠지만, 내가 트리를 써야 할 일이 있다면...
위와 같이 고민을 하다가, 라이브러리를 찾겠지. -_-;
( 내가 특별한 상황에 있지 않는 이상 Reinvention 할 필요는 없겠지 )
마지막으로 인터넷을 검색하다가, 트리에 대한 좋은 글들이 있는 블로그를 발견했다.
http://sweeper.egloos.com/category/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0/page/3
나는 머 내 맘대로 날림 수준으로 복습해 놓은거지만,
이 분은 상당히 자세히 적어 두었다.
하나 더, http://webdiis.unizar.es/asignaturas/EDA/AVLTree/avltree.html 에 가면
Self-Balancing Binary Search Tree 과정을 시각적으로 볼 수 있다.
(2012.7.4 추가)
self-balancing search tree 의 대표적인 두 가지 방법
AVL Tree 와 RB(red-black) Tree 중 어느 것이 좋은가?
실제 나의 기억으로도 자료 구조 시간에 저 두 개의 트리에 대해서 집중적으로 배운거 같긴 하다.
결론부터 말하면 RB Tree 를 더 선호하는 것 같다.
실제로 Java 의 TreeMap 과 C++ STL std::map 에서 self-balancing search tree 의 구현은 모두
RB Tree 로 되어 있다고 한다.
http://stackoverflow.com/questions/5288320/why-is-stdmap-implemented-as-red-black-tree
위 글의 답변을 인용해 보면,
AVL Tree 는 최대 1.44 lg(n) 이지만 RB Tree 는 최대 2 lg(n) 이라고 한다.
그럼에도 불구하고, RB Tree 를 쓰는 이유는
삽입/삭제 후의 Re-balancing 에 드는 코스트 때문이란다.
AVL Tree 의 경우 O(lg n) 이지만, RB Tree 는 O(1) 이다.
그래서 빈번한 RB Tree 가 search 에 조금 약 할지라도,
삽입/삭제에서 훨씬 강하니... RB Tree 를 선택한게 아닐까?
(2012.7.5 추가)
둘 다 구현하다가 시간 문제로 포기.
아.. 학교다닐 때 열심히 할 껄... 이라는 생각도 해 봤지만,
어짜피 기억 안나는건 같았을껄?
AVL 은 Balacing-Factor 를 가지고 Re-balancing 을 하고,
RB Tree 는 red-black properties 에 따라 Re-balancing 을 한단다.
후.. 나중에 필요하면 다시 공부하자.
* RB-Tree 는 http://en.wikipedia.org/wiki/Red%E2%80%93black_tree 에
상세하게 설명되어 있다. 약간만 더 손보면 되는 코드와 함께!
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 11장 그래프(Graph) (0) | 2012.07.10 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |
글
Eclipse CDT + Cygwin 으로 C/C++ 개발 환경 설정 관련...
Windows 에서 C/C++ 개발환경 설정을 위해 Eclipse CDT 를 선택하기로 하고 설치해서 사용하는데,
그냥은 잘 안된다. 그래서 이것저것 삽질한 내용을 남겨본다.
( Visual Express C++ 2010 은 회사에서 쓸 수 없고,
Dev-C++ 은 개발중단된지 오래되어서 Eclipse + Cygwin 조합을 사용했다)
1. 필요한 프로그램 설치
Eclipse CDT - http://www.eclipse.org/downloads/ 에서 Eclipse IDE for C/C++ Developers 설치
eclipse 는 단순히 압축풀면 끝.
Cygwin - http://www.cygwin.com 에서 setup.exe 를 받아서 설치.
필요한 패키지는 gcc-core, gcc-g++, make, gdb, binutils 정도?
이것만 선택하면 추가로 필요한 패키지는 알아서 설치된다.
2. 전역 환경 설정
메뉴의 Window > Preferences 에서 설정가능하다.
반드시 필요한 설정은
- C/C++ > Build > Build Variables 에서 Show system variables 를 선택하여
PATH 에서 c:\cygwin\bin 을 제일 위로 바꿀것.
(이걸 안하면 빌드시 에러가 나는 경우가 있는 듯 하다)
- C/C++ > Debug > Source Lookup Path 에서 'Add' 하여 'Path Mapping' 선택
왼쪽엔 \cygdrive\d 오른쪽엔 D:\ 라고 적고 추가한다.
(소스가 저장되는 드라이브에 따라 d 를 c 나 다른 문자로 바꾸면 된다.
이걸 하지 않으면 Debug 시에 소스가 보이지 않는다. 또한 gcc 실행시에도 문제가 생기는 듯.. )
- tab 대신 space 를 사용하려면 tab, formatter 검색해서 설정 필요.
- 파일 인코딩 관련해서 설정하려면 encoding 검색해서 설정하면 된다.
3. 프로젝트 생성
여러가지 프로젝트 타입이 있던데, 보통은 C or C++ Project > Makefile project 로 선택하면 무난 할 듯.
Toolchins 는 Cygwin GCC 를 선택해야 겠지.
4. 프로젝트 설정
실제 사용을 위해서는 몇 가지 셋팅이 더 필요했는데...
먼저 메뉴의 Project > Properties 로 들어간다.
- Makefile 을 자동 생성하게 하려면 C/C++ Build 에서 'Generate Makefiles automatically' 를 체크하자.
(이걸 체크 하지 않고 직접 makefile 을 작성해도 될 거 같은데... 실제로 아직 해보질 않아서 패스..)
- C/C++ > Environment 에서 PATH 를 보면 c:\cygwin\usr\bin 이 제일 앞에 있다면 삭제해 버리거나
c:\cygwin\bin 으로 바꾸어 주자.
(이걸 안하면 make 에서 에러가 발생하는데... 역시 이유는 잘 모르겠다)
p.s
음.. 일단 이렇게 하면 문제는 없지만,
Segmentation fault 에러 났을 때, GDB 가 출력하는 메시지를 제대로 파싱을 못하는 지,
제대로 디버깅이 안된다. 후우... 아직 해결방법을 못 찾았다..
'프로그래밍' 카테고리의 다른 글
| Dynamic Programming - Building Bridges, Balanced Partition. (2) | 2012.08.06 |
|---|---|
| Dynamic Programming - Longest Increasing Subsequence, Box Stacking (0) | 2012.08.03 |
| Dynamic Programming - Make Change Problem (2) | 2012.08.01 |
| Dynamic Programming - Maximal Contiguous Subsequent Sum Problem (2) | 2012.07.31 |
| Dynamic Programming - Knapsack Problem (0) | 2012.07.31 |
글
C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables)
8장 해쉬 테이블이다.
(책에는 해시 테이블이라고 적혀 있지만, 난 해쉬가 어감이 더 좋아서...)
바로 고고싱...
해쉬 테이블(hash table)
해쉬 테이블은 키(key)라는 특별한 인덱스로 자료에 접근하는 배열로 구성되는 자료구조 이다.
해쉬 테이블의 해쉬 함수는 키 값을 받아 그 키의 해쉬값(hash coding 또는 hash value)을 리턴한다.
간단한 해쉬테이블을 시각적으로 표시했을 때, 아래와 같은 그림으로 표시할 수 있다.

(Author: Jorge Stolfi, 원본: http://en.wikipedia.org/wiki/File:Hash_table_3_1_1_0_1_0_0_SP.svg)
해쉬 테이블의 장점은 상수 시간에 탐색이 가능한 것이다.
대신 다른 특징(혹은 단점?)은 순차적인 접근을 지원하지 않는 것이다.
따라서 이러한 특징에 맞는 상황에서 사용되어야 할 것이다.
추가적으로 해쉬 테이블의 특징을 좀 더 알아보자.
- 사용할 키와 해쉬 함수를 잘 선택하여 테이블에 균등하게 항목이 배분되도록 해야 한다.
- 다른 키값에 대해 같은 해쉬값(같은 테이블로 매핑되는 경우)을 가지는 경우 충돌(collision)이라고 한다.
- 충돌 해결 방법에는 여러가지가 있으며 대표적인 방법(책에 설명된)은
연쇄 해쉬 테이블(chained hash table)과 개방 주소지정 해쉬 테이블(open-addressed hash table)이 있다.
위키피디아에 따르면 해쉬 테이블은 탐색 트리(search tree)나 다른 lookup 구조의 테이블보다 효율적이라고 한다.
이런 이유로 아래와 같은 곳에서 사용이 된다. (참조: http://en.wikipedia.org/wiki/Hash_table#Uses )
- Associative arrays (프로그래밍 랭귀지의 데이터 타입 같은 것. 예를 들면 Python 의 Dictionary 타입?)
- Database indexing
- Caches
- Sets
- Object representation
- Unique data representation
위키피디아에 상세한 설명이 되어 있으니, 해쉬 테이블에 대한 더 많은 정보를 원한다면 방문해 보기 바란다.
http://en.wikipedia.org/wiki/Hash_table
앞으로 나올 용어에 대해서 간단히 설명하면 다음과 같이 사용할 것이다.
n : 테이블의 항목 갯수
m : 버킷의 갯수
a : 부하 계수(load factor). a = n / m
해쉬 테이블 인터페이스
해쉬 테이블에 필요한 인터페이스는 간단한 편이다.
Data Insert, Remove, Lookup 정도?
중요한 건 키 값을 같이 넘겨주는 것이다.
해쉬 함수(hash function)
해쉬 함수 h 는 키값 k 를 받아 테이블 위치 x 에 매핑하는 함수이다.
k 의 값은 보통 정수임을 가정한다.
k 가 정수가 아니더라도 어렵지 않게 정수로 바꿀 수 있다.
(물론 k 가 같은 값이 나오지 않게 잘 바꿔야 하겠다)
책에서는 간단한 방법 2가지를 제시한다.
- 나눗셈 방법(devision method)
으로 표현할 수 있다. 일반적으로 m 의 값으로는 2의 제곱수는 피해서
2의 제곱수에 가깝지 않은 소수를 m 으로 선택한다.
- 곱셈 방법(multiplication method)
k*A 한 다음 여기에서 소수 부분만 택하여 m 을 곱한값에서 정수 부분만 택한값을 사용한다.
( A 값은 저렇게 하면 효율적이라고 Donald Knuth 란 분이 이야기 했나 보다. )
이것들은 간단한 방법들이니 좀 더 효율적인 해쉬 함수를 원한다면,
좀 더 공부가 필요하겠다.
충돌 해결(Collision resolution)
출동 해결 방법에는 여러가지가 있다.
좀 더 자세한 건 역시 위키피디아! ( http://en.wikipedia.org/wiki/Hash_table#Collision_resolution )
- 연쇄 해쉬 테이블(Sererate Chaining)

(Author: Jorge Stolfi, http://en.wikipedia.org/wiki/File:Hash_table_5_0_1_1_1_1_0_LL.svg )
위 그림과 같이 한 버킷을 링크트 리스트로 구성하는 방법이다.
- 개방 주소지정 해쉬 테이블(Open addressing)

(Author: Jorge Stolfi,http://en.wikipedia.org/wiki/File:Hash_table_5_0_1_1_1_1_0_SP.svg )
그림이 좀 헷갈려 보이긴 하지만, 위와 같은 충돌 발생시 다른 버킷에 저장하는 방식이다.
여기서 잠깐, 다른 버킷은 어떻게 선택하는가?
잘 알려진 방법으로는 다음과 같은 3가지 방법이 있다.
1. 선형 조사(Linear probing) : 다음 버킷을 조사. 주클러스터링 현상으로 과다한 조사 발생 가능성 있음.
2. 2중 조사(Quadratic probing) : i^2 번째의 버킷을 조사. 부클러스터링 현상으로 과다한 조사 발생 가능성 있음.
(i 는 현재까지 조사한 위치의 갯수)
3. 2중 해싱(Double hashing): 해쉬 함수와 보조 해쉬 함수의 결과를 더하는 것이다.
2중 조사와 다른 점은, 키 값에 따라 다음 조사위치가 고정된 것이 아니라 달라진다는 것이다.
수식으로 표현하지면 위와 같다. 그러나 어떤 위치가 두 번 조사되기 전에 모든 위치들이
조사됨을 보장하기 위해 다음의 두 절차 중 하나를 따라야 한다.
a. m이 2의 제곱수이고 h2 가 항상 홀수를 리턴한다.
b. m이 소수이고 h2는 항상 m보다 작은 양수를 리턴해야 한다.
결론
여기에 적은 것은 해쉬 테이블의 일부분일 뿐이다.
이 글에서는 해쉬 테이블의 핵심만 기억하도록 하자.
해쉬 테이블의 정의, 좋은 해쉬 함수가 필요하다는 거, 그리고 충돌 해결이 필요하다는 거 정도?
역시 중요한 것은 실제로 적절한 곳에 사용하는 것이겠지...
해쉬 테이블에 대한 깊이 있는 이해를 위해서는 좀 더 공부가 필요하겠다.
(2012.7.2 추가)
Double Hashing이 항상 좋은 것은 아니다.
예를 들면 Double Hashing 함수에서 i 값이 증가 할 때, 그 interval 이 커서
cache 문제가 발생할 수 있다고 한다.
(참고: http://en.wikipedia.org/wiki/Double_hashing )
또한, 인터넷을 검색해서 적절한 second hash function 의 샘플을찾지를 못하겠다. 나중에 꼭 쓸일이 있게되면 연구해 봐야겠다.
(2012.7.3)
굳이 인터넷을 검색하지 않아도,
책에 적절한 Double Hashing 의 적절한 샘플이 있었다.
(어젠 책이 없는 관계로...)
이 식에서 아래와 같은 방법의 해쉬 함수를 사용할 수 있다.
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2012.07.03 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 5장 연결 리스트(linked list) (0) | 2012.06.20 |