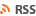검색결과 리스트
공부에 해당되는 글 19건
- 2012.07.10 C 로 구현한 알고리즘 - 2부 자료 구조, 11장 그래프(Graph)
- 2012.07.03 C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue)
- 2012.07.03 C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree)
- 2012.06.27 C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables)
- 2012.06.21 C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set)
- 2012.06.20 C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue)
- 2012.06.20 C 로 구현한 알고리즘 - 2부 자료 구조, 5장 연결 리스트(linked list)
- 2012.06.19 C 로 구현한 알고리즘 - 1부 준비, 4장 알고리즘 분석
- 2012.06.14 C 로 구현한 알고리즘 - 1부 준비, 3장 재귀 2
글
C 로 구현한 알고리즘 - 2부 자료 구조, 11장 그래프(Graph)
AVL 트리와 RB 트리 공부하다가 진이 빠져서, 몇 일 책을 못봤다.
결국 RB 트리를 구현하긴 했지만, 왜 했나 싶기도 하고...
이번엔 자료구조의 마지막 장, Graph 이다.
시작
|
(출처: http://en.wikipedia.org/wiki/File:6n-graf.svg )
위 그림이 컴퓨터 사이언스에서 이야기 하는 Graph 자료구조를 그림으로 표현한 것이다.
그림에는 따로 방향성이 없는데, 방향성을 가지는 (즉, 가운데 선이 화살표 모양으로 표시될 수 있는)
Graph 도 있다.
Graph는 객체들 사이의 관계나 연결에 따라 정의되는 문제들을 모델링하는 데 주로 사용된다.
객체는 정점(Vertex)으로 표시되고 객체들 사이의 관계나 연결은 정점들 정점들 사이의 에지(Edge)로 표현된다.
그래프의 탐색방법은 Vertex 를 특성 순서로 방문하는 기법이다.
여기에는 Breadth-First Search(BFS)와 Depth-First Search(DFS)가 있다.
이 글에서는 Graph 와 Graph traversal(그래프 탐색방법)에 대해서 알아 볼 것이다.
그래프는 다음과 같은 어플리케이션에서 사용된다.
- 그래프 알고리즘
- 네트워크 홉(hop) 세기- 위상 정렬: 예를들면, 와우의 스킬트리를 Linear List 로 만드는 것이랄까...
- 그래프 색칠하기: 각 Edge로 연결된 Vertex는 서로 다른 색을 칠하는 문제. 이 기준을 만족시키는 최소의 색 수를
Chromatic number라 한다.
- 해밀턴 사이클 문제: 한 Vertex에서 출발하여 모든 Vertex들을 한 번씩만 방문하여 시작 Vertex로 돌아오는 사이클을
해밀턴 사이클 이라고 한다.
TSP(Traveling Salesman Problem, 외판원 여행 문제)가 해밀턴 사이클 문제의 특수한 경우.
- 클릭 문제: Clique(클릭)이란, Undirected Graph 'G' 의 Vertex들로 이루어진 집합이 있을 때, 이 집합의 임의의
두 Vertex가 모두 Edge로 연결되어 있다면 이 집합을 Clique이라 한다.
예를들면, 오각형 안에 별이 그려져 있는 그래프를 생각해 보라.
- 충돌 직렬화: (설명이 좀 힘들어 패스. 사실 나도 어렴풋이 감이 오는 정도이기도 하고..;;)
그래프(Graph)
Graph는 두 가지 요소, Vertex와 Edge로 이루어진다.
Vertex는 객체를 의미하고 Edge는 객체들 사이의 관계나 연결을 말한다.
또한 Graph는 Directed(방향성)/Undirected(무방향성)이 있다.
Directed Graph는 Edge를 화살표로 표시한다. 때로는 이 Edge를 Arc라고 부르기도 한다.
Directed Graph에서 Cycle이 없는 Graph를 Directed Acyclic Graph(DAG)라고 한다.
Edge는 라벨이나 숫자값과 같은 Edge value를 가질 수도 있다.
Graph의 기본 인터페이스는 다음 링크에서 확인 할 수 있다.
http://en.wikipedia.org/wiki/Graph_%28data_structure%29#Operations
(Vertex 추가/삭제 인터페이스도 필요하다면 추가를 해야 할 것이다)
Graph는 두 개의 다른 자료구조료 표현할 수 있다.
List 와 Matrix 이다.
두 개의 큰 차이는 Adjacent vertex들를 List로 표현하는가 Matrix로 표현하는가의 차이이다.
List로 표현하는 방법은 쉽게 머리속에 상상할 수 있다. (Adjacency List)
Matrix로 표현하는 방법은 아래 그림과 같다. (Adjacency Matrix)
 |
|
(출처: http://en.wikipedia.org/wiki/Adjacency_matrix#Examples )
그림과 같은 Row 1 은 Vertex 1 와 연결된 Adjacent vertex들을 나타낸다.
Undirected Graph는 Matrix가 대칭적으로 나타난다.
Directed Graph에서 1 --> 2 라면, (Row 1, Col 2)는 1 이고, (Row 2, Col 1)은 0 이 될 것이다.
이 두가지는 어떤 차이점이 있을까?
| Adjacency list | Adjacency Matrix |
|
| 저장공간 |
O(V+E) |
O(V^2) |
| Vertex 추가 |
O(1) | O(V^2) |
| Edge 추가 |
O(1) | O(1) |
Vertex 삭제 |
O(E) |
O(V^2) |
| Edge 삭제 |
O(E) | O(1) |
Vertex u와 v가 인접한가? (단, u와 v의 저장위치는 알고 있다) |
O(V) | O(1) |
| 특징 | Vertex나 Edge를 삭제할 때, 모든 Vertex들이나 Edge들을 찾아야 할 필요가 있다. 일반적으로 Sparse graph에 효율적이다. |
Vertex를 추가/삭제하기 위해서는, Matrix가 Resize/Copy되어야 하므로 느리다.
graph가 dense할 때 사용한다. ( E가 V^2에 가까울 수록... ) |
(V는 Vertex들의 갯수, E는 Edge들의 갯수)
그래프 탐색(Graph traversal)
Graph의 Vertex들을 특정 순서대로 한 번씩 방문하는 것을 말한다.
여기에는 두 가지 방법이 있는 데, 너비 우선(Breadth-first) 탐색과 깊이 우선(Depth-first) 탐색이 있다.
- Breadth-First Search(BFS)
Graph 를 더 탐험하기 전에 한 정점에 인접한 정점들을 먼저 방문하는 것이다.
|
(Author: Alexander Drichel, 출처 : http://en.wikipedia.org/wiki/File:Breadth-first-tree.svg )
위 Graph의 Vertex에 적힌 숫자가 방문 순서이다.
BSF는 최소 신장 트리(minimum spanning trees)와 최단 경로(shortest paths) 등, 많은 어플리케이션에 유용하다.
그 외에도 http://en.wikipedia.org/wiki/Breadth-first_search#Applications 여기에서 여러가지 적용의 예를 볼수 있다.
BSF의 구현을 Pseudocode 로 작성해 보면 다음과 같다.
G: a graph, v: root of G
(All verties are colored with white at starting)
function BFS(G, v):
Queue Q;;
v.setColor(gray);
Q.enqueue(v);
while ( NOT Q.isEmpty() )
t = Q.dequeue();
t.setColor(black);
for each ( x in G.adjacentVerties(t) )
if ( x.getColor() == white )
o.setColor(gray);
Q.enqueue(o);
- Depth-First Search(DFS)
Graph를 탐색할 때, 한 브랜치를 따라 가능한 멀리까지 먼저 방문하는 것이다.
 |
(Author: Alexander Drichel, 출처:http://en.wikipedia.org/wiki/File:Depth-first-tree.svg )
DFS는 사이틀 탐지(cycle detection)와 위상 정렬(topological sorting)을 포함한 많은 어플리케이션에 유용하다.
그 외에도 http://en.wikipedia.org/wiki/Depth-first_search#Applications 여기에서 다른 적용 예를 볼 수 있다.
특히 DFS를 이용하여 미로를 만드는 것은 비디오로 감상해 볼 수 있다.
DFS의 구현을 Pseudocode 로 작성해 보면 다음과 같다.
G: a graph, v: root of G
(All verties are colored with white at starting)
function DFS(G, v):
v.setColor(gray);
for each ( x in G.adjacentVerties(v) )
if ( x.getColor() == white )
call DFS(G, x);
v.setColor(black)
결론
Graph 자체는 별로 어렵지 않은 듯 한데...
책에도 적혀 있듯이, 아주 유연한 자료구조이다.
그래서인지 Java API 에도 STL 에도 Graph 자료구조는 없다.
이 후의 Graph 알고리즘에서 좀 더 사용해보면 익숙해 지겠지..
'공부' 카테고리의 다른 글
| [알고리즘] P, NP, NP-Complete, NP-Hard (0) | 2012.07.16 |
|---|---|
| C 로 구현한 알고리즘 - 3부 알고리즘에 들어가기 전에... (1) | 2012.07.16 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
글
C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue)
힙과 우선순위 큐도 별로 어렵진 않다.
물론 깊이 들어가면 어려운건 매 한가지지만.
어쨌거나 기본적인 개념은 어려운것이 아니니...
힙(Heap)
위키피디아의 정의에 따르면,
힙이란 힙 속성(heap property)를 만족하는 특별한 트리 기반의 자료 구조란다.
힙 속성(heap property)란?
만약 B 가 A 의 자식 노드라면, key(A) >= key(B)를 만족하는 것이다.
좀 더 쉽게 말하면 가장 큰 값을 가지는 노트가 항상 Root 가 되는 것이다.

( Author: Ermishin, http://en.wikipedia.org/wiki/File:Max-Heap.svg )
위 그림과 같은 예가 힙이다.
힙은 모든 항목들이 정렬되는 것이 목표가 아니라, 가장 크거나 작은 항목만 빨리 찾을 때 좋은 자료 구조이다.
힙은 왼쪽 평형을 이루기 때문에 노드가 추가 될 때, 트리는 단계별로 왼쪽부터 채워진다.
그리고 이런 힙을 표현하는 좋은 방법은 배열에 저장하는 것이다.
왼쪽 평형을 이루는 트리를 배열에 저장할 때의 장점은
힙의 마지막 노드의 위치를 빨리 알 수 있게 되는것이다.
( 힙에서 데이터를 삽입 할 때, 삽입 위치는 마지막 노드의 다음 노드에 삽입한 후,
연산을 시작하기 때문에 이것은 중요하다. )
또한 i 번째 노드의 부모의 위치는 floor((i-1)/2),
자식의 위치는 2i+1, 2i+2 로 찾기 쉬운 장점도 있다.
힙의 인터페이스는 insert 와 extract 정도...
임의의 data 를 delete 하는 인터페이스는 없다.
우선순위 큐(Priority Queue)
우선순위 큐는 힙과 동일하다. 그리고 힙의 인터페이스를 그대로 사용하면 된다.
거기에 peek 인터페이스만 추가하면 된다.
힙의 변종들(Variants)
위키피디아에는 여러 힙의 변종들이 있는데...
역시나 그 힙들의 각각이 특징을 다 외우지는 못하겠다.
http://en.wikipedia.org/wiki/Heap_%28data_structure%29#Comparison_of_theoretic_bounds_for_variants
위 링크에 보면 여러 힙들의 Time Complexities 가 표로 작성되어 있는데,
큰 데이터를 다뤄야 하는 경우라면, 상황에 따라서 가장 중요한 연산의 복잡도를 고려하여
여러 힙 중에서 적절한 것을 고르면 되겠다.
기타
자료 집합을 힙으로 만들 때,
모든 원소에 대해서 heap_insert() 를 하게 되면 O(n lg n) 의 복잡도를 가지게 된다.
이것을 O(n) 의 복잡도로 실행할 수 있다.
루트의 위치가 floor(n/2)-1 에서 0까지인 트리를 힙으로 계속 만들어 가면 된다고 한다.
( 사실 무슨 말인지 모르겠다. 실제 예제를 가지고 확인해 보면 좋겠다 )
이렇게 되면 O(lg n)시간에 실행되는 floor(n/2)-1 개의 연산이 있지만,
힙 만드는 과정의 절반만이 두 단계 이상의 자료 비교를 필요로 하므로 전체적인 실행시간은
O(n) 이 된다고 한다.
(2012.7.4 추가)
자료 집합을 힙으로 만들 때, O(n) 시간에 해결하는 방법은...
마지막 노드를 가지고 있는 부모 노드로 부터 - Root 의 인덱스가 0 일 때, floor(n/2)-1 번 위치부터
Root 로 가면서 Heapfy 하는 것이다.
처음에는 원소가 2개 혹은 3개를 가진 트리 형태를 전부 Heapfy 하고,
그 윗 단계로 가게 되면, extract 이후에 Reheapfy 하는 과정..
즉, Root 와 그 자식들을 비교해서 Heapfy 하는 과정을 계속 반복하는 것이다.
결론
기본 힙은 쉬운거 같다.
근데 힙의 Variants 들도 참 많다.
각 Variants 들의 특징도 한번씩 살펴보면 좋겠지만.. 시간이 될까?
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 3부 알고리즘에 들어가기 전에... (1) | 2012.07.16 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 11장 그래프(Graph) (0) | 2012.07.10 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
글
C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree)
트리에 대한 자료를 찾으면서 우선 위키피디아를 한 번 쭉 읽어 봤다.
그 중 바이너리 트리의 마지막 부분(http://en.wikipedia.org/wiki/Binary_tree#External_links)을 보면
'Trees in computer science' 를 보면 엄청난 종류의 트리들이 나온다.
이걸 보면서 느낀 건, "아, 정말 사람들이 치열하게 고민을 했구나...' 하는 것이다.
약간의 성능 향상이라도 얻기 위해 이 부분, 저 부분 고민을 한 흔적이 느껴졌다.
( 이 수많은 트리들이 그냥 나온건 아니니깐... )
마음 같아선 저 모든 트리들의 특징을 정리해 보고 싶지만... 그건 힘들것 같고,
일반적으로 트리를 사용하는 이유(효율적인 탐색!!!)에 집중해서 정리해 본다.
트리(Tree)
먼저 아래 그림을 보자.
( http://en.wikipedia.org/wiki/File:Binary_tree.svg )
이미지로 표현을 하자면 위와 같은 모양으로 자료가 저장되는 자료구조가 트리(Tree)다.
트리에서 사용하는 용어들은 다음과 같다.
- 노드(Node): 위 그림에서 데이터 및 다른 데이터를 가리키는 포인터를 포함해서 노드(Node)라고 한다.
- 루트(Root): 트리에서 제일 상위에 있는 노드를 루트라고 한다.
- 자식(Child): 한 노드의 바로 아래(포인터를 가지고 있는) 노드를 말한다.
- 부모(Parent): 한 노드의 바로 상위 노드를 말한다.
- 분기 계수(branching factor): 한 노드가 가질 수 있는 자식의 최대 수를 말한다.
- 형제(sibling): 부모의 다른 자식 노드들이다.
- 자손(descendant): 한 노드에서 뻗어나간 하위의 모든 노드들을 말한다.
- 조상(ancestor): 한 노드와 루트 간의 경로에 있는 모든 노드들이다.
- 높이(height): 노드들이 존재하는 단계의 수. 트리의 높이. 예를 들면 위 그림의 높이는 4 이다.
- 리프 노드(Left Node): 자식이 없는 노드.
기본적인 용어들은 머 이 정도?
트리는 다음과 같은 곳에서 사용된다.
- 허프만 코딩: 자료 집합을 압축하는데 사용하는데 허프만 트리를 사용하는 자료 압축 방법
- 프로그램 메뉴
- 데이터베이스 시스템
- 식 처리: 컴파일러나 휴대용 계산기에서 자주 수행되는 작업이다.
- 우선순위 큐
이 글의 이후 내용은 다음과 같은 내용을 다루겠다.
- 바이너리 트리(Binary Tree, 이진트리)
- 순회 방법(Travesal)
- 트리 평형,
- 바이너리 서치 트리(BST, Binary Serarch Tree, 이진탐색트리)
- 그 외 주제에 대해서
바이너리 트리(Binary Tree, 이진 트리)
자식을 2개까지 가질 수 있는 노드들로 이루어진 트리다.
광범위하게 사용되며, 더 복잡한 트리 구조체의 토대도 된다.
순회 방법들(Traversal)
트리의 노드들을 방문하는 순서에 대한 내용이다.
- preorder (전위 순회) : Parent -> Left -> Right
- inorder (중위 순회) : Left -> Parent -> Right
- postorder (후위 순회) : Left -> Right -> Parent
앞에 접두사가 현재 노드의 방문 순서를 가리킨다고 생각하면 된다.
그리고 노드의 방문은 Recursive 하게 방문한다.
바이너리 서치 트리(Binary Search Tree, BST, 이진 탐색 트리)
탐색을 위해 특별히 구조화된 이진 트리이다.
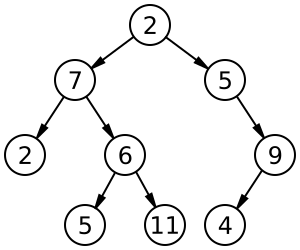
부모보다 작은 노드는 왼쪽 자손에 부모보다 큰 노드는 오른쪽 자손에 위치한다.

( http://en.wikipedia.org/wiki/File:Binary_search_tree.svg )
예를 들면, 위 그림과 같이 트리를 구성하게 된다.
BST 의 탐색 속도는 트리가 평형을 유지한다면 O(lg n)이 된다.
(트리 평형을 이룬다는 말은 트리의 주어진 노드의 갯수에 대해 트리의 높이를 짧게 유지한다는 것이다)
트리가 균형을 이루지 못한다면 최악의 경우 O(n)이 된다.
이 차이는 매우 큰 데, 2^16 개의 데이터를 검색할 때
O(lg n)는 최대 16번, O(n)은 최대 65,536번의 탐색이 필요하다.
여기까지는 솔직히 별로 어렵지 않다.
하지만 트리의 평형을 어떻게 유지하는 가에 대한 문제로 들어가면 쉽지 않다.
트리 평형(Tree Balancing)
위에서 잠깐 언급했듯이,
트리 평형이란 주어진 노드들의 개수에 대해 트리의 높이를 가능한 짧게 유지하는 것이다.
트리의 평형은 데이터 서치의 성능에 영향을 미친다.
바이너리 트리에 노드를 Insert, Delete 할 때, Balancing 을 유지하는 트리에는 여러 방법이 있다.
이러한 트리들을 Self-balancing binary search tree 라고 한다.
( http://en.wikipedia.org/wiki/Self-balancing_binary_search_tree )
위키피디아에는 위와 같은 트리들에 대해서 언급하고 있다.
Selft-balancing binary search tree 들 중 하나 정도는 외우고 싶은데,
머가 제일 쉬운지 모르겠다.
그 외 트리에 대해...
- 수식의 표현
바이너리 트리는 탐색에 특화된 것으로 보이지만,
다른 곳에도 응용이 가능하다.
예를 들면 수식을 표현하는 데, 좋은 방법이 된다.
- 트라이(Trie)
가변 길이 문자열 집합을 탐색하는 데 주로 사용된다.

( http://en.wikipedia.org/wiki/File:Trie_example.svg )
- B-Tree
( B-Tree 는 Binary Tree 가 아니다. 혼동하지 말자. )
보조 기억장치에 저장된 자료에 접근하는 성능을 향상시키기 위해서
대체로 데이터베이스 시스템에서 사용하는 탐색 트리다.
B-Tree에 대한 자세한 내용은 http://en.wikipedia.org/wiki/B-tree 을 참고.결론
글의 처음에 이야기 했듯이 많은 종류의 트리들이 있다.
그리고 각각의 트리들은 저마다 특징이 있다.
많은 종류덕에 이 특징들을 모두 기억하기도 쉽지 않다.
내가 생각하는 트리의 핵심은 이거다.
1. 데이터의 크기를 비교할 수 있는 데이터를 검색하는 데는 바이너리 서치 트리가 좋다.
2. 바이너리 서치 트리라면 가능하면 기본적으로 Self-balancing 이 되도록 해야 한다.
3. 다뤄야 하는 데이터의 갯수가 많다면, 그 때의 상황에 맞는 특화된 트리를 찾아본다.
4. 탐색과 관계없는 자료도 트리로 표현하는 게 좋을 때가 있다. (수식이나 디렉토리, 메뉴 처럼...)
이게 정답은 아닐수도 있겠지만, 내가 트리를 써야 할 일이 있다면...
위와 같이 고민을 하다가, 라이브러리를 찾겠지. -_-;
( 내가 특별한 상황에 있지 않는 이상 Reinvention 할 필요는 없겠지 )
마지막으로 인터넷을 검색하다가, 트리에 대한 좋은 글들이 있는 블로그를 발견했다.
http://sweeper.egloos.com/category/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0/page/3
나는 머 내 맘대로 날림 수준으로 복습해 놓은거지만,
이 분은 상당히 자세히 적어 두었다.
하나 더, http://webdiis.unizar.es/asignaturas/EDA/AVLTree/avltree.html 에 가면
Self-Balancing Binary Search Tree 과정을 시각적으로 볼 수 있다.
(2012.7.4 추가)
self-balancing search tree 의 대표적인 두 가지 방법
AVL Tree 와 RB(red-black) Tree 중 어느 것이 좋은가?
실제 나의 기억으로도 자료 구조 시간에 저 두 개의 트리에 대해서 집중적으로 배운거 같긴 하다.
결론부터 말하면 RB Tree 를 더 선호하는 것 같다.
실제로 Java 의 TreeMap 과 C++ STL std::map 에서 self-balancing search tree 의 구현은 모두
RB Tree 로 되어 있다고 한다.
http://stackoverflow.com/questions/5288320/why-is-stdmap-implemented-as-red-black-tree
위 글의 답변을 인용해 보면,
AVL Tree 는 최대 1.44 lg(n) 이지만 RB Tree 는 최대 2 lg(n) 이라고 한다.
그럼에도 불구하고, RB Tree 를 쓰는 이유는
삽입/삭제 후의 Re-balancing 에 드는 코스트 때문이란다.
AVL Tree 의 경우 O(lg n) 이지만, RB Tree 는 O(1) 이다.
그래서 빈번한 RB Tree 가 search 에 조금 약 할지라도,
삽입/삭제에서 훨씬 강하니... RB Tree 를 선택한게 아닐까?
(2012.7.5 추가)
둘 다 구현하다가 시간 문제로 포기.
아.. 학교다닐 때 열심히 할 껄... 이라는 생각도 해 봤지만,
어짜피 기억 안나는건 같았을껄?
AVL 은 Balacing-Factor 를 가지고 Re-balancing 을 하고,
RB Tree 는 red-black properties 에 따라 Re-balancing 을 한단다.
후.. 나중에 필요하면 다시 공부하자.
* RB-Tree 는 http://en.wikipedia.org/wiki/Red%E2%80%93black_tree 에
상세하게 설명되어 있다. 약간만 더 손보면 되는 코드와 함께!
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 11장 그래프(Graph) (0) | 2012.07.10 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |
글
C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables)
8장 해쉬 테이블이다.
(책에는 해시 테이블이라고 적혀 있지만, 난 해쉬가 어감이 더 좋아서...)
바로 고고싱...
해쉬 테이블(hash table)
해쉬 테이블은 키(key)라는 특별한 인덱스로 자료에 접근하는 배열로 구성되는 자료구조 이다.
해쉬 테이블의 해쉬 함수는 키 값을 받아 그 키의 해쉬값(hash coding 또는 hash value)을 리턴한다.
간단한 해쉬테이블을 시각적으로 표시했을 때, 아래와 같은 그림으로 표시할 수 있다.

(Author: Jorge Stolfi, 원본: http://en.wikipedia.org/wiki/File:Hash_table_3_1_1_0_1_0_0_SP.svg)
해쉬 테이블의 장점은 상수 시간에 탐색이 가능한 것이다.
대신 다른 특징(혹은 단점?)은 순차적인 접근을 지원하지 않는 것이다.
따라서 이러한 특징에 맞는 상황에서 사용되어야 할 것이다.
추가적으로 해쉬 테이블의 특징을 좀 더 알아보자.
- 사용할 키와 해쉬 함수를 잘 선택하여 테이블에 균등하게 항목이 배분되도록 해야 한다.
- 다른 키값에 대해 같은 해쉬값(같은 테이블로 매핑되는 경우)을 가지는 경우 충돌(collision)이라고 한다.
- 충돌 해결 방법에는 여러가지가 있으며 대표적인 방법(책에 설명된)은
연쇄 해쉬 테이블(chained hash table)과 개방 주소지정 해쉬 테이블(open-addressed hash table)이 있다.
위키피디아에 따르면 해쉬 테이블은 탐색 트리(search tree)나 다른 lookup 구조의 테이블보다 효율적이라고 한다.
이런 이유로 아래와 같은 곳에서 사용이 된다. (참조: http://en.wikipedia.org/wiki/Hash_table#Uses )
- Associative arrays (프로그래밍 랭귀지의 데이터 타입 같은 것. 예를 들면 Python 의 Dictionary 타입?)
- Database indexing
- Caches
- Sets
- Object representation
- Unique data representation
위키피디아에 상세한 설명이 되어 있으니, 해쉬 테이블에 대한 더 많은 정보를 원한다면 방문해 보기 바란다.
http://en.wikipedia.org/wiki/Hash_table
앞으로 나올 용어에 대해서 간단히 설명하면 다음과 같이 사용할 것이다.
n : 테이블의 항목 갯수
m : 버킷의 갯수
a : 부하 계수(load factor). a = n / m
해쉬 테이블 인터페이스
해쉬 테이블에 필요한 인터페이스는 간단한 편이다.
Data Insert, Remove, Lookup 정도?
중요한 건 키 값을 같이 넘겨주는 것이다.
해쉬 함수(hash function)
해쉬 함수 h 는 키값 k 를 받아 테이블 위치 x 에 매핑하는 함수이다.
k 의 값은 보통 정수임을 가정한다.
k 가 정수가 아니더라도 어렵지 않게 정수로 바꿀 수 있다.
(물론 k 가 같은 값이 나오지 않게 잘 바꿔야 하겠다)
책에서는 간단한 방법 2가지를 제시한다.
- 나눗셈 방법(devision method)
으로 표현할 수 있다. 일반적으로 m 의 값으로는 2의 제곱수는 피해서
2의 제곱수에 가깝지 않은 소수를 m 으로 선택한다.
- 곱셈 방법(multiplication method)
k*A 한 다음 여기에서 소수 부분만 택하여 m 을 곱한값에서 정수 부분만 택한값을 사용한다.
( A 값은 저렇게 하면 효율적이라고 Donald Knuth 란 분이 이야기 했나 보다. )
이것들은 간단한 방법들이니 좀 더 효율적인 해쉬 함수를 원한다면,
좀 더 공부가 필요하겠다.
충돌 해결(Collision resolution)
출동 해결 방법에는 여러가지가 있다.
좀 더 자세한 건 역시 위키피디아! ( http://en.wikipedia.org/wiki/Hash_table#Collision_resolution )
- 연쇄 해쉬 테이블(Sererate Chaining)

(Author: Jorge Stolfi, http://en.wikipedia.org/wiki/File:Hash_table_5_0_1_1_1_1_0_LL.svg )
위 그림과 같이 한 버킷을 링크트 리스트로 구성하는 방법이다.
- 개방 주소지정 해쉬 테이블(Open addressing)

(Author: Jorge Stolfi,http://en.wikipedia.org/wiki/File:Hash_table_5_0_1_1_1_1_0_SP.svg )
그림이 좀 헷갈려 보이긴 하지만, 위와 같은 충돌 발생시 다른 버킷에 저장하는 방식이다.
여기서 잠깐, 다른 버킷은 어떻게 선택하는가?
잘 알려진 방법으로는 다음과 같은 3가지 방법이 있다.
1. 선형 조사(Linear probing) : 다음 버킷을 조사. 주클러스터링 현상으로 과다한 조사 발생 가능성 있음.
2. 2중 조사(Quadratic probing) : i^2 번째의 버킷을 조사. 부클러스터링 현상으로 과다한 조사 발생 가능성 있음.
(i 는 현재까지 조사한 위치의 갯수)
3. 2중 해싱(Double hashing): 해쉬 함수와 보조 해쉬 함수의 결과를 더하는 것이다.
2중 조사와 다른 점은, 키 값에 따라 다음 조사위치가 고정된 것이 아니라 달라진다는 것이다.
수식으로 표현하지면 위와 같다. 그러나 어떤 위치가 두 번 조사되기 전에 모든 위치들이
조사됨을 보장하기 위해 다음의 두 절차 중 하나를 따라야 한다.
a. m이 2의 제곱수이고 h2 가 항상 홀수를 리턴한다.
b. m이 소수이고 h2는 항상 m보다 작은 양수를 리턴해야 한다.
결론
여기에 적은 것은 해쉬 테이블의 일부분일 뿐이다.
이 글에서는 해쉬 테이블의 핵심만 기억하도록 하자.
해쉬 테이블의 정의, 좋은 해쉬 함수가 필요하다는 거, 그리고 충돌 해결이 필요하다는 거 정도?
역시 중요한 것은 실제로 적절한 곳에 사용하는 것이겠지...
해쉬 테이블에 대한 깊이 있는 이해를 위해서는 좀 더 공부가 필요하겠다.
(2012.7.2 추가)
Double Hashing이 항상 좋은 것은 아니다.
예를 들면 Double Hashing 함수에서 i 값이 증가 할 때, 그 interval 이 커서
cache 문제가 발생할 수 있다고 한다.
(참고: http://en.wikipedia.org/wiki/Double_hashing )
또한, 인터넷을 검색해서 적절한 second hash function 의 샘플을찾지를 못하겠다. 나중에 꼭 쓸일이 있게되면 연구해 봐야겠다.
(2012.7.3)
굳이 인터넷을 검색하지 않아도,
책에 적절한 Double Hashing 의 적절한 샘플이 있었다.
(어젠 책이 없는 관계로...)
이 식에서 아래와 같은 방법의 해쉬 함수를 사용할 수 있다.
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 10장 힙(Heap)과 우선순위 큐(Priority Queue) (0) | 2012.07.03 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree) (0) | 2012.07.03 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 5장 연결 리스트(linked list) (0) | 2012.06.20 |
글
C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set)
후... 파폭 버그인지 글쓰다가 날려먹었다.
게다가 실수로 임시저장본까지 날려먹었다.
그냥 다시 쓰자...
집합(Set)
( set.h, set.c )
고등학교 수학시간에 배운 집합을 기억한다면 기본은 다 되었다.
그래도 일단 굳이 정의를 하자면 아래와 같다.
"집합은 서로 다른 원소들의 순서 없는 모임이다."
필요한 인터페이스도 수학시간에 다 배운것들이다.
교집합, 합집합, 차집합, 부분집합인가?, 같은집합인가? 등...
예제에서는 집합을 LInked List 로 구현을 했다.
이러면 탐색에 시간이 많이 걸린다.
(책에서도 예제의 구현은 많이 않은 자료의 집합에 적당하다고 한다)
집합을 구현하는 방법으로 해쉬테이블이나 이진트리를 사용하면
탐색에 걸리는 시간을 줄일 수 있을것이다.
집합의 인터페이스
http://en.wikipedia.org/wiki/Set_%28computer_science%29#Operations
위 링크에서 집합에 필요한 인터페이스를 확인할 수 있다.
집합을 사용하는 것
- 집합 커버(set covering)
이름만으로는 무엇인지 이해하기 어렵다. 책에는 다음과 같이 적혀있다.
조합론(combinatorics)와 자원 선택 등 많은 문제들을 잘 모델링하는 최적화 문제이다.
이 말도 어렵기는 마찬가지이다. 책에서 설명하는 예를 보자.
여러 명의 선수들이 있다. 이 선수들은 각각 임의의 기술들을 가지고 있다.
기술의 종류는 기술1 ~ 기술n 까지 있으며, 이 모든 기술들을 커버(covering)할 수 있는 팀을 구성하고자 한다.
위 문제를 일반화 시켜보면,
집합 S 는 커버할 원소의 집합(기술1 ~ 기술n)이다.
집합 P 는 S 의 부분집합의 집합(선수1 ~ 선수m)이다. 각 선수는 임의의 기술들을 가지고 있다.
집합 C 는 커버집합(모든 기술을 커버할 수 있는 팀)이다.
위와 같이 집합이 사용된다.
여기에서 좀 더 나아가, Set Covering Problem 에 대해서 이야기 해 보자면,
이 문제는 NP-complete 문제이다.
그래서 예제( cover.h, cover.c )에서는 Greedy 알고리즘으로 문제를 해결한다.
- 그래프
그래프를 표현하는 가장 일반적인 방법은 인접한 점들의 리스트를 사용하는 데,
이 인접한 점들의 리스트를 표현하는 한 가지 방법이 인접한 점들을 집합으로 표현하는 것이다.
- 그 외
자료 상관 관계(두 자료의 교집합, 차집합 등을 파악...)
집합에 대한 수학(큰 수에 대한 수학 연산들...)
그래프 알고리즘(정점이나 에지(edge)들을 함께 모으는데 사용...)
관계 대수(데이터베이스 시스템의 이론적인 질의(query) 언어이다...)
기타 등등...
관련 주제들
- 벤 다이어그램
집합의 연산의 결과를 시각적으로 결정하는 데 도음이 되는 그림 표현
- 비트 벡터(Bit-vector) 표현
전체집합이 작고, 그냥 알수 있는(?) 경우에 유용한 집합 표현이다.
전체집합에서 각 원소를 한 비트로 표현하는 것이다.
( 원소의 값을 가지고 있는게 아니고 0/1 로만 표현되므로, 그냥 알수 있는(?) 경우라는 표현을 쓴 것이다 )
- 다중집합(multisets)
원소의 중복을 허용하는 집합이다.
결론
위에서도 말했듯이 고등학교 수학시간에 배운 집합을 기억한다면,
수학적 이론에 대한 것은 더 공부할 필요가 없다.
( 졸업한지가 벌써 ...년이 지났어도 기억하는 걸 보면 어렵지도 않은 내용이다 )
집합은 여러가지 방법으로 구현할 수 있으므로,
해당 상황에 가장 효율적인 방법을 사용하면 되겠다.
http://en.wikipedia.org/wiki/Set_%28computer_science%29#Implementations_2
위 링크에서 집합의 구현에 대한 이야기를 추가로 볼 수 있다.
이상 끝.
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 9장 트리(Tree) (0) | 2012.07.03 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 5장 연결 리스트(linked list) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 1부 준비, 4장 알고리즘 분석 (0) | 2012.06.19 |
글
C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue)
스택과 큐도 링크드 리스트만큼 쉽다.
컨셉만 이해하고 넘어가면 될듯.
스택(Stack)
( stack.h, stack.c )
스택은 자료를 LIFO(last-in, fist-out)방식으로 처리한다.
가장 쉬운 예로는 접시가 있겠다.
접시를 쌓고(push), 접시를 꺼내는(pop) 행동에서
일반적으로 가장 마지막에 쌓은 접시를 제일 먼저 사용한다.
이것이 LIFO 인 것이다.
대표적인 사용의 예는
C 에서 함수 호출, 추상 스택 머신 등이 있다.
큐(Queue)
( queue.h, queue.c )
큐는 스택과 반대로 FIFO(fist-in, first-out)방식으로 자료를 처리한다.
줄을 서서 서비스를 받기위해 기다리는 사람들을 생각하면 되겠다.
대표적인 사용의 예는
세마포어에서 자원을 기다리는 프로세스들을 큐로 관리하는 것,
이벤트 처리, 생산자-소비자 문제등이 있다.
기타
좀 더 확장된 자료구조로는 다음과 같은 것들이 있다.
데크(double-ended queues: deques)는 head / tail 양쪽에서 삽입과 삭제가 가능한 큐이다.
원형 큐(circular queues)는 tail을 갖지 않고 마지막 항목이 head 로 연결되는 큐이다.
결론
스택과 큐는 간단하지만 매우 중요한 자료구조이다.
큐의 경우, 일반적으로 프로세스/쓰레드 간 데이터를 주고 받는데 많이 사용하는데,
두 프로세스/쓰레드가 동시에 큐에 엑세스하지 않도록 하는 장치가 필요할 것이다.
별 내용이 없네... 머 쉬운거니깐.
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 5장 연결 리스트(linked list) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 1부 준비, 4장 알고리즘 분석 (0) | 2012.06.19 |
| C 로 구현한 알고리즘 - 1부 준비, 3장 재귀 (2) | 2012.06.14 |
글
C 로 구현한 알고리즘 - 2부 자료 구조, 5장 연결 리스트(linked list)
1부 준비가 끝나고 2부 자료구조의 시작이다.
알고리즘과 자료구조는 뗄 수 없는 관계니깐...
그 첫 번째로 연결 리스트(linked list)다.
연결 리스트라니.. 번역이 좀 그렇다.. 한글+영어가 좀 어색하네..
그냥 아래에서는 영문 그대로 적겠다.
솔직히 전산쪽 용어들은 오히려 그게 더 명확하니깐...
이 책에서 사용하는 소스코드들은
http://www.hanb.co.kr/exam/1063/
에서 다운받을 수 있다. 각 장에서 사용하는 소스파일 명은 중간중간 적어 두겠다.
링크드 리스트에는 다음과 같은 것들이 있다.
- 싱글 링크드 리스트 (single-linked list)
단일 연결 리스트. 각 항목들이 하나의 포인터로 연결된 가장 단순한 리스트.
![]()
(출처: http://en.wikipedia.org/wiki/Linked_list )
- 더블 링크드 리스트 (double-linked list) - 이중 연결 리스트
각 항목들이 두개의 포인터로 연결된 리스트. 양쪽 방향으로 포인터를 가지고 있다.
![]()
(출처: http://en.wikipedia.org/wiki/Linked_list )
- 서큘러 리스트 (circular list) - 원형 리스트
마지막 항목의 포인터가 NULL 대신에 첫 항목을 가리키는 연결 리스트. 리스트를 원형으로 순회할 수 있다.

(출처: http://en.wikipedia.org/wiki/Linked_list )
링크드 리스트를 사용하는 예에는 다음과 같은 것들이 있다.
메일링 리스트, 리스트(GUI 컴포넌트), 다항식, 메모리 관리(할당 가능한 메모리 영역 관리), LISP,
다른 자료구조들의 구현(스택, 큐, 집합, 해시 테이블, 그래프 등...)
예제 파일들
( list.h, list.c / dlist.h, dlist.c / clsit.h, clist.c )
상황에 따라 적절한 인터페이스가 추가/삭제가 될 수 있겠지만,
예제의 헤더 파일에서 기본적으로 필요한 인터페이스를 확인할 수 있다.
결론
책에서는 꽤 길게 설명을 해 두었지만,
링크드 리스트는 제일 쉬운 자료구조이다.
딱히 장황하게 적을 필요가 없다고 본다.
여기서부터 각 인터페이스에 대한 복잡도를 표시해 두었는데,
비단 링크드 리스트 뿐만 아니라, 다른 자료 구조에 대한
인터페이스의 복잡도도 알아두면 효율적으로 프로그램을 작성하는데 도움이 될 것이다.
Linked List 는 종종 Array 와 같은 다른 형태의 리스트와 비교되는데,
http://en.wikipedia.org/wiki/Linked_list
위 사이트의 글을 참고하면 되겠다.
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 1부 준비, 4장 알고리즘 분석 (0) | 2012.06.19 |
| C 로 구현한 알고리즘 - 1부 준비, 3장 재귀 (2) | 2012.06.14 |
글
C 로 구현한 알고리즘 - 1부 준비, 4장 알고리즘 분석
이번엔 4장 알고리즘 분석 복습...
아마도 '재귀' 알고리즘 이후에 알고리즘 분석 챕터가 있는 것은,
이 챕터를 좀 더 이해하기 쉽게 하기 위해서인가 보다.
그렇다 하더라고 학교 수업에 들었던 기억을 떠 올리면, 꽤 지루했던게 기억난다.
알고리즘을 사용할 때, 그 알고리즘의 성능을 이해하는 것은 중요하다.
문제를 해결하기 위해 여러가지 알고리즘을 선택할 때도 효율적인 알고리즘을 선택할 수 있고,
또한, 어떻게 적절하게 사용할 것인지 계획을 세우는 데도 도움이 된다.
(책에서는 Garbage Collection 을 예로 들고 있다. 여기에 사용되는 알고리즘은 많은 시간이
필요하기 때문에, 적당한 순간에만 사용하도록 해야한다. )
최악분석
알고리즘의 최악의 경우에 대한 성능을 분석하는 것이다.
여기에는 4가지 이유가 있는데,
1. 많은 알고리즘이 대부분의 실행에서 최악의 성능을 보인다. 예를들면, 탐색에서 원하는 자료를 찾지 못하는 경우...
2. 많은 알고리즘이 최상의 경우에 똑같은 성능을 보인다.
3. 평균 성능을 계산하는 것이 쉽지 않은 경우가 있다.
4. 최악의 경우는 성능의 상위 한계를 의미한다. 즉 분석 결과보다 더 나쁘게 실행되지는 않는다는 것을 보장한다.
(내 생각에는 1, 4번이 제일 중요한듯...)
예외적으로 평균 성능을 근거로 해야 하는 경우는 있다. (예를들면, 퀵 정렬 같은 무작위 알고리즘)
O-표기법
이것은 알고리즘의 성능을 정형적으로 표현하는 가장 일반적인 표기법인다.
이것은 알고리즘의 복잡도(complexity)를 표현한다.
자료가 커짐에 따라, 성능이 어떻게 나빠지는지 나타내는지 보여준다고 생각하면 될 듯.
일반적으로 단순하게 아래와 같이 알고리즘의 복잡도를 표시한다.
(실제로는 상수를 포함한 식으로 표시된다. )
( 일반적인 복잡도와 거기에 해당하는 예. 복잡도가 낮은 순으로. n 은 자료의 갯수. )
| 복잡도 | 예 |
O(1) |
자료 집합에서 첫번째 항목을 가져오는 것 |
O(lg n) |
자료 집합을 반으로 나누고 그 반을 다시 반으로 나누는 과정을 반복 |
O(n) |
자료 집합을 순회하기 |
| O(n lg n) |
자료 집합을 반복해서 둘로 나누고 나뉘어진 반을 순회하는 것 |
O(n^2) |
한 집합의 각 자료에 대해 같은 크기의 다른 집합을 순회하는 것 |
| O(n^2) | 집합의 모든 부분집합을 생성하는 것 |
O(n!) |
집합의 모든 순열을 생성하는 것 |
(증가율을 표한한 그래프. 가로는 n = 자료의 크기, 세로는 T(n) = 알고리즘의 실행 시간을 나타냄.)

* 적절한 그래프 이미지를 찾지 못해 엑셀에서 직접 작업.
가로/세로 축, 각 그래프 선에 대해서 레이블을 쓰고 싶은데, 옵션을 못 찾겠음.. (없는건지..)
결론
특이한 경우가 아니면, 현업에서 이미 알려진 알고리즘에 대해서 알고리즘 복잡도를 분석할 이유가 없다.
각 알고리즘에 대해서 어느 정도의 성능을 나타내는가를 알고 있으면 된다고 생각한다.
우리가 할 수 있는것은 저 복잡도 계산에서 과다한 상수를 포함하지 않도록 하여
알고리즘이 효율적으로 동작하도록 하는 정도?
중요한 것은 위에서도 언급했듯이, 적절한 알고리즘을 적절하게 사용하는 것이다.
(적어놓고 나니 애매한데, 어쨌거나 현업에서는 여러가지 변수가 존재하니깐...)
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 5장 연결 리스트(linked list) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 1부 준비, 3장 재귀 (2) | 2012.06.14 |
글
C 로 구현한 알고리즘 - 1부 준비, 3장 재귀
최근에 어떤 계기로 미루고 미뤄왔던 알고리즘 공부를 시작했다.
대학 다닐 때 알고리즘 수업 2번 연속 출석미달로 'F' 받았던터라, 늘 찜찜했는데...
알고리즘을 공부하기 위해 선택한 책은 "C 로 구현한 알고리즘" 이다.
왜냐하면... 나름 오라일리 책인데다가... 회사에 굴러다녀서 살 필요가 없어서...;
대충 1장 소개랑 2장 포인터 다루기는 패스하고
3장 재귀부터 복습 겸 글을 남겨본다.
개본적 재귀(recursion)
문제를 자신보다 점점 더 작은 인스턴스들로 정의할 수 있게 하는 강력한 원리이다.
전산에서는 자신을 호출하는 재귀 함수를 사용해서 재귀적으로 정의된 문제들을 해결한다.
Depth 가 깊어지면 스택 오버플로우의 위험이 크다.
현업에서 실제로 이런 형태를 쓰면 안되겠지.
꼬리 재귀(tail recursion)
컴파일러가 최적의 코드를 만들어 낼 수 있는 재귀의 형태이다.
재귀 호출이 함수 몸체의 제일 마지막에 실행되는 문장이고,
리턴값이 다른식에 사용되지 않는 형태이다.
다시 말해면 재귀함수 호출한 뒤에 수행할 명령이 없어야 한다는거?
(이런 형태는 굳이 Iteration 하게 정의해서 풀 수도 있지만,
재귀 형태가 머랄까.. 좀 더 문제를 푸는 방법을 명확히 나타내는 듯 하다.
요새는 컴파일러가 똑똑해져서 최적화 옵션을 주면
꼬리 재귀도 알아서 Iteration 하게 만들어 준다니깐.. 머.)
팩토리얼 값을 구하기 위한 기본적 재귀와 꼬리 재귀
(빨갛게 표시한 부분을 주목)
따로 부연설명은 하지 않겠다.
기본적 재귀 |
꼬리 재귀 |
int fact (int n) {
return 1; else if (n == 1) return 1; else return n * fact (n-1); } |
int facttail (int n, int a) { if (n < 0) return 0; else if (n == 0) return 1; else if (n == 1) return 1; else return facttail (n-1, n*a); } |
주의사항
재귀함수는 반드시! 하나 이상의 종료조건이 있어야 하며,
재귀호출이 이 종료조건에 도달할 수 있어야 한다.
그렇지 않다면 스택 오버플로우~
결론
꼬리 재귀에 대한 좀 더 명확한 이해를 할 수 있었고,
이제 더 정확히 알고 사용할 수 있을꺼 같다.
이상 끝.
'공부' 카테고리의 다른 글
| C 로 구현한 알고리즘 - 2부 자료 구조, 8장 해쉬 테이블(hash tables) (0) | 2012.06.27 |
|---|---|
| C 로 구현한 알고리즘 - 2부 자료 구조, 7장 집합(Set) (0) | 2012.06.21 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 6장 스택과 큐(Stack and Queue) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 2부 자료 구조, 5장 연결 리스트(linked list) (0) | 2012.06.20 |
| C 로 구현한 알고리즘 - 1부 준비, 4장 알고리즘 분석 (0) | 2012.06.19 |